Unveiling The Power Of Karnaugh Maps: A Comprehensive Guide To Boolean Simplification

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification

The realm of digital circuits thrives on the manipulation of binary logic, where the intricate dance of "ones" and "zeros" orchestrates the flow of information. At the heart of this intricate dance lies Boolean algebra, a powerful tool for expressing and simplifying logic functions. While Boolean equations provide a precise mathematical representation, their complexity can hinder understanding and efficient implementation. This is where the Karnaugh map, often abbreviated as K-map, emerges as a visual and intuitive aid, transforming complex Boolean expressions into simplified, optimized forms.

A Visual Journey into Boolean Simplification:

Imagine a map not of geographical landscapes, but of the logic space defined by Boolean variables. This is the essence of a Karnaugh map. It represents a truth table, a tabular representation of all possible input combinations and their corresponding outputs, in a visually appealing and insightful manner. Each cell in the map corresponds to a unique input combination, and the cell’s content reflects the output value for that combination.

The brilliance of the Karnaugh map lies in its arrangement. Unlike a conventional truth table, where input combinations are listed in a sequential order, the K-map’s cells are organized based on their adjacency. Adjacent cells differ by only one variable, creating a visual representation of the relationship between input combinations. This arrangement, coupled with a specific labeling scheme, facilitates the identification of patterns and simplifications within the logic function.

Deciphering the Map:

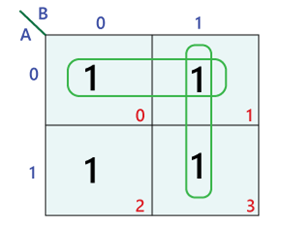
A typical K-map is a grid composed of squares, with each square representing a unique input combination. The number of squares in the map is determined by the number of input variables. For example, a map with two input variables (A and B) will have four squares, representing the combinations (0,0), (0,1), (1,0), and (1,1).

The map’s rows and columns are labeled with the input variables, with each row or column representing a specific value of the variable. The labeling follows a specific pattern, ensuring that adjacent cells differ by only one variable. This pattern is crucial for identifying simplification opportunities.

Unveiling the Power of Simplification:

The core strength of the K-map lies in its ability to simplify Boolean expressions, reducing them to their most compact and efficient forms. This simplification is achieved by identifying groups of adjacent cells containing "1" values, signifying the presence of logical terms that can be combined. These groups, known as "minterms," represent the essential building blocks of the simplified logic function.

The process of simplification involves identifying the largest possible groups of adjacent "1" cells, including both horizontally and vertically adjacent cells, as well as those that wrap around the edges of the map. The larger the group, the fewer variables are required in the corresponding term, leading to a more efficient implementation.

Beyond Simplification: Unveiling Insights:

The K-map’s benefits extend beyond simplification. It provides a visual representation of the logic function, aiding in understanding its behavior and identifying potential problems or inconsistencies. It can also be used to analyze and optimize existing circuits, ensuring they operate efficiently and meet the desired functionality.

FAQs: Demystifying the K-map

1. What are the limitations of the K-map?

While powerful, K-maps are best suited for functions with a limited number of input variables. As the number of variables increases, the map’s complexity grows exponentially, making it cumbersome to manage and analyze. For functions with more than six variables, alternative methods like Quine-McCluskey minimization or computer-aided tools are often preferred.

2. Can K-maps be used for functions with multiple outputs?

Yes, K-maps can be used for functions with multiple outputs. Each output function is represented by a separate K-map, allowing for independent simplification and optimization.

3. How do you handle "don’t care" conditions in a K-map?

"Don’t care" conditions arise when certain input combinations are irrelevant or not defined for the function. These conditions can be represented by an "X" in the K-map. During simplification, "don’t care" conditions can be included in groups of adjacent "1" cells, maximizing simplification and further reducing the complexity of the logic function.

4. What are some real-world applications of K-maps?

K-maps find widespread applications in digital circuit design, particularly in the simplification of logic functions for:

• Combinational circuits: These circuits produce an output based solely on the current input values, with no memory of past inputs. Examples include adders, decoders, and multiplexers.
• Sequential circuits: These circuits incorporate memory elements, allowing their output to depend on both current and past inputs. Examples include counters, registers, and state machines.

Tips for Mastering the K-map:

• Start with small examples: Begin by simplifying functions with two or three variables to understand the basic principles and mechanics of the K-map.
• Practice, practice, practice: The key to mastering K-maps lies in consistent practice. Work through various examples and exercises to develop familiarity and proficiency.
• Visualize the logic: Instead of merely memorizing rules, strive to understand the underlying logic behind the simplification process. This will enhance your ability to apply the K-map effectively.
• Utilize available tools: Several online tools and software packages are available to generate and analyze K-maps, providing a convenient way to visualize and simplify logic functions.

Conclusion: A Powerful Tool for Digital Design

The Karnaugh map, with its intuitive visual representation and powerful simplification capabilities, remains an indispensable tool for digital circuit designers. It empowers them to translate complex Boolean expressions into optimized logic functions, leading to efficient circuit implementations. By understanding the principles and techniques associated with K-maps, designers can effectively tackle the challenges of Boolean simplification, paving the way for the creation of robust, efficient, and reliable digital systems.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Boolean Simplification. We hope you find this article informative and beneficial. See you in our next article!