Demystifying Karnaugh Maps: A Visual Approach To Boolean Logic Simplification

Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Related Articles: Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Introduction

With great pleasure, we will explore the intriguing topic related to Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

The realm of digital logic design often involves manipulating complex Boolean expressions, which can become unwieldy as the number of variables increases. Enter the Karnaugh map, a visual tool that simplifies this process, making it easier to identify and express minimal logic functions. This article delves into the intricacies of Karnaugh maps, exploring their construction, application, and significance in digital circuit optimization.

What are Karnaugh Maps?

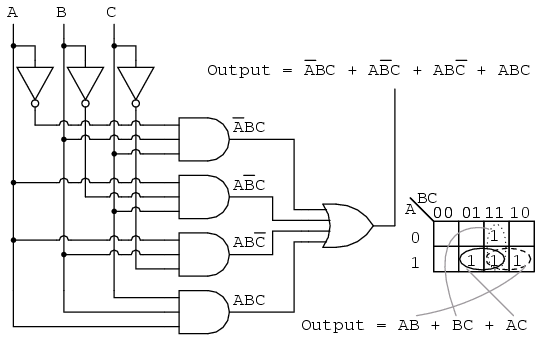
Karnaugh maps, often referred to as K-maps, are graphical representations of Boolean functions, providing a visual framework for simplifying Boolean expressions. They are essentially truth tables rearranged into a grid format, where each cell represents a unique combination of input variables. The arrangement of cells is strategically designed to facilitate the identification of adjacent cells with identical output values, known as "adjacencies." These adjacencies are key to simplifying Boolean expressions, as they represent common terms that can be combined using Boolean algebra laws.

Constructing a Karnaugh Map: A Step-by-Step Guide

Building a Karnaugh map involves a systematic process that ensures accurate representation of the Boolean function. The following steps outline the construction process:

1. Determine the Number of Variables: Identify the number of input variables in the Boolean function. This determines the size of the Karnaugh map. For instance, a function with three variables requires a 2×4 grid, while a four-variable function necessitates a 4×4 grid.

2. Assign Binary Values to Cells: Each cell in the Karnaugh map represents a unique combination of input variable values. The binary values are assigned in a specific order, ensuring that adjacent cells differ by only one variable. This ordering is crucial for identifying adjacencies.

3. Label Rows and Columns: The rows and columns of the Karnaugh map are labeled with the binary values of the input variables. The labeling scheme ensures that adjacent cells differ by only one bit.

4. Populate the Map with Output Values: For each cell, determine the corresponding output value of the Boolean function based on the input variable combination represented by that cell. This is achieved by evaluating the function for the specific input values.

Simplifying Boolean Expressions Using Karnaugh Maps: A Visual Approach

The true power of Karnaugh maps lies in their ability to simplify Boolean expressions. This simplification process leverages the concept of adjacencies, where adjacent cells with identical output values represent common terms that can be combined. The following steps illustrate this simplification process:

1. Identify Adjacencies: Scan the Karnaugh map for groups of adjacent cells with identical output values. These groups can be horizontal, vertical, or diagonal, and they should always contain a power of two number of cells (1, 2, 4, 8, etc.).

2. Formulate Minimal Sum-of-Products Expressions: Each adjacency represents a common term that can be expressed as a product of literals. The product term is formed by combining the variables that are constant within the adjacency group.

3. Combine Adjacencies: Adjacencies can be combined to form larger groups, further simplifying the expression. The goal is to cover all the "1" cells in the map with the smallest possible number of groups.

4. Write the Final Expression: Once all adjacencies are identified and combined, the simplified Boolean expression is formed by summing the product terms representing each group.

Applications of Karnaugh Maps: Beyond Simplification

Karnaugh maps are not limited to simplifying Boolean expressions. They find applications in various aspects of digital logic design:

• Circuit Optimization: Simplified Boolean expressions directly translate to optimized digital circuits with fewer gates, reducing cost, power consumption, and complexity.

• Logic Design Implementation: Karnaugh maps aid in designing and implementing logic circuits using various logic gates, ensuring minimal gate count and efficient circuit operation.

• Troubleshooting and Debugging: By analyzing the Karnaugh map, designers can identify potential errors in logic circuits and troubleshoot issues related to incorrect output behavior.

• Conversion between Logic Forms: Karnaugh maps facilitate the conversion between different logic forms, such as Sum-of-Products (SOP) and Product-of-Sums (POS), enabling designers to choose the most suitable form for their specific application.

Advantages of Karnaugh Maps: A Powerful Tool for Logic Design

Karnaugh maps offer several advantages over traditional Boolean algebra methods for simplifying expressions:

• Visual Approach: The visual representation of the function makes it easier to identify adjacencies and simplify expressions compared to manipulating complex algebraic equations.

• Intuitive and User-Friendly: The grid format and simple rules for identifying adjacencies make Karnaugh maps accessible to designers with varying levels of experience.

• Reduced Complexity: Karnaugh maps effectively handle Boolean functions with a moderate number of variables, simplifying the design process without resorting to complex algebraic manipulations.

• Optimized Circuit Design: The simplification process leads to optimized logic circuits with fewer gates, reducing cost, power consumption, and complexity.

Limitations of Karnaugh Maps: Addressing the Trade-offs

While Karnaugh maps are powerful tools, they also have limitations:

• Limited to Small Number of Variables: Karnaugh maps become cumbersome for functions with more than five variables, as the grid size increases exponentially.

• Subjective Interpretation: The process of identifying adjacencies and combining groups can be subjective, potentially leading to different interpretations and simplified expressions.

• Manual Process: The simplification process is primarily manual, requiring designers to carefully examine the map and identify adjacencies.

FAQs: Addressing Common Questions About Karnaugh Maps

Q: What is the maximum number of variables a Karnaugh map can handle effectively?

A: Karnaugh maps are typically effective for functions with up to five variables. Beyond that, the grid size becomes too large and the process becomes cumbersome.

Q: How do I handle "don’t care" conditions in a Karnaugh map?

A: "Don’t care" conditions represent input combinations where the output value is irrelevant. These conditions are marked with an "X" in the map and can be used to simplify expressions by including them in adjacencies.

Q: Can I use Karnaugh maps for functions with more than five variables?

A: While Karnaugh maps are not practical for functions with more than five variables, other methods like Quine-McCluskey algorithm can be used for simplification.

Q: What are some common mistakes to avoid when using Karnaugh maps?

A: Common mistakes include:

• Incorrectly labeling rows and columns: Ensure that the binary values are assigned in the correct order to facilitate adjacency identification.
• Overlooking adjacencies: Carefully scan the map to identify all possible adjacencies, including diagonal ones.
• Incorrectly combining adjacencies: Ensure that the groups you form contain a power of two number of cells and represent valid combinations of input variables.

Tips for Effective Karnaugh Map Usage: Maximizing the Tool’s Potential

• Start with a clear understanding of the Boolean function: Define the function accurately before constructing the Karnaugh map.

• Use a systematic approach for labeling and populating the map: Follow the guidelines for binary value assignment and output value determination.

• Visualize adjacencies clearly: Use different colors or markers to highlight adjacencies and make them easily identifiable.

• Check for minimal groups: Ensure that you are using the smallest possible number of groups to cover all the "1" cells in the map.

• Verify your simplified expression: Double-check that the simplified expression accurately represents the original Boolean function.

Conclusion: Karnaugh Maps – A Cornerstone of Digital Logic Design

Karnaugh maps remain a valuable tool in digital logic design, offering a visual approach to simplifying Boolean expressions and optimizing logic circuits. Their intuitive nature, user-friendliness, and effectiveness in handling functions with a moderate number of variables make them a staple in the design process. While limitations exist, particularly for functions with a large number of variables, Karnaugh maps continue to play a crucial role in digital circuit design, enabling efficient implementation and optimization. As technology advances, the principles behind Karnaugh maps continue to inspire new methods for simplifying Boolean expressions and enhancing the design of complex digital systems.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. We thank you for taking the time to read this article. See you in our next article!